Scale-Bridging Modelling and Designing New Materials in a “Virtual Lab”

Motivation

One challenge of modern materials science is to find new functional materials (such as magnets, superconductors and mechanically robust alloys) with better performance. Theoretical simulations have proven to be very helpful in this respect by providing a sort of “virtual lab” environment (as illustrated in the diagram below) where one can study different materials, make predictions about their properties based on computer simulations and find ways of improving their properties much faster than in a physical laboratory setting. The underlying equations describing any material are those of quantum mechanics where the behaviour of all interacting electrons and atomic nuclei in the material can be, in principle, predicted almost exactly. However, for realistic models of materials, the quantum-mechanical calculations are too expensive, even for modern supercomputers, and hence simpler so-called effective models become necessary to study the systems that comprise those materials on different length scales, bridging the microscopic (atomic scale) and macroscopic (device scale) descriptions. This article gives a brief overview of different steps of scale-bridging modelling in the context of magnetic materials. (More in-depth information is available in the references [1], [2] and [3]).

Scale-bridging Methodology and Examples

1. Electronic Properties

When it comes to studying a particular material, the minimal information that should be provided as input for computer simulations is its crystal structure and chemical composition. From this, it is possible to write down the full quantum Hamiltonian of the system that can be solved using, for example, density functional theory (DFT). The latter makes it possible to calculate, so far approximately but quite accurately, the key electronic properties of the system, such as whether it is metallic or insulating, what kind of chemical bonding it has and whether there are finite magnetic moments. The sole reason why DFT only gives approximate results for the calculation of ground-state properties at present is that the exact expression for the exchange-correlation functional is not known yet. However, there are a number of well-established approximations to this functional which have been thoroughly tested over recent decades, for example, local-spin density and generalised-gradient approximations, with which quantities like equilibrium crystal volume and magnetisation can be predicted within a 5% deviation from the measured values. Also, in the case of transition metal systems where correlations can be moderate or strong, the description of electronic properties can be much improved by using dynamical mean-field theory (DMFT) on top of DFT, which is the idea of the DFT+DMFT method [4]. The resulting electronic properties can change in terms of bandwidth and lifetime of electronic states which has impact on all the other properties, especially the magnetic ones, as elaborated upon, for example, in recent work [5].

In the next step, since we are interested in magnetic properties on the larger scale, interactions between the atomic magnetic moments are calculated using the Lichtenstein- Katsnelson-Antropov-Gubanov (LKAG) approach [6] for different pairs of atomic moments at varying distances. The computational efficiency of this approach is characterised by the fact that one can use the chemical unit cell of the chosen system to address the magnetic interactions at much larger distances. For example, for ferromagnetic iron where the interatomic distance is around 2.8 Å, interactions for distances up to 15 Å can be calculated routinely and reliably using the RSPt software [7,8] where the LKAG approach is available. Such calculations would otherwise require large supercells, leading to high computational costs. The limiting value of real-space distance between interacting spins which can be treated in the LKAG method is largely determined by the number of k-points in the reciprocal space that are used in the DFT calculation: the magnetic interactions for larger distances converge to stable values for a sufficiently fine k-mesh. From the top graph above, which is plotted for the simple example of iron, one can see close-to-linear scaling of the calculation time with the total number of k-points. This is to be expected since the magnetic interaction between two spins is evaluated from a sum over different k-points, which should also theoretically be parallelisable almost linearly with respect to the number of cores. In the bottom graph, however, one can observe linear scaling for up to around 256 cores, which was tested with the RSPt code. For a larger number of cores, there is a considerable decrease in parallelisation efficiency, most likely due to additional overhead time, for example, internode connections. For systems that are more complex than iron, one can expect better scaling, that is, up to a higher number of cores. For example, we looked at the Co/Pt(111) system from [5] where the Co monolayer is magnetic and is located on the Pt(111) surface. In the graph below, the inverse computational time is plotted versus the number of cores for the calculation of exchange parameters for this system on the Tetralith supercomputer at the National Supercomputing Centre (NSC) in Linköping (1,800 k-points) as well as on the old and new nodes of the Dardel system at PDC for 1,800 and 6,075 k-points. (The old nodes refer to Dardel nodes before the interconnect upgrades in early 2023 and the new nodes refer to the nodes after the upgrade to Slingshot 11.) Here one can observe better scaling with respect to the number of cores and k-points than for iron, leading to parallelisation benefits even for 1,024 cores.

Since electronic correlations in certain systems can be more complicated than in iron, advanced methods like DFT+DMFT might be necessary to calculate the magnetic interactions more accurately. In recent work [5], it was demonstrated how important such correlation effects can be for different types of systems (including Co/Pt(111) mentioned above), and their possible origins in terms of electronic properties were discussed.

2. Atomistic spin dynamics

Once reliable values of magnetic interaction parameters are obtained, one can construct an effective spin model, such as the Heisenberg or extended Heisenberg model, that abstracts away from the electronic description of the system and pictures every atom as a well-defined magnetic moment that interacts with its neighbours. The model then describes the magnetic energy of the system due to these interactions and makes it possible to calculate the torques acting on each spin if the system is out of equilibrium. Based on that and the Landau-Lifshitz-Gilbert (LLG) equation, one can simulate the time evolution of all the magnetic moments as the system moves towards equilibrium, which is the main subject of atomistic spin dynamics (see book [1]). This can be useful when searching for an equilibrium magnetic configuration. An example is shown on the cover which depicts the spin-spiral magnetic state of a Mn monolayer on a W(110) surface obtained from simulated annealing using the UppASD software [1]. In this method, one starts from a random magnetic configuration in a large supercell with thousands or even millions of spins (see the next section for further details on computational scaling) at high temperature and then calculates the spin dynamics while gradually lowering the temperature of the system until, for example, zero temperature is reached. The system usually ends up in one of the many local energy minima which can represent some of the features of the actual lowest energy state; in this case, it is the spin-spiral stripe- shaped domains that are at 90 degrees to each other and can coexist because they have the same energy. These domains have also been measured in experiments [9] on a similar length scale of a few nanometres. As discussed, for example, in review [3], longer annealing time can help to get closer to the lowest energy state in annealing simulations. In the case of Mn/W(110), this increases the fraction of spin-spiral domains of a certain orientation, that is, it makes the system closer to a single-domain state. In general, for more complicated systems (especially with frustrated magnetic interactions), the problem of finding the global energy minimum is highly non-trivial and simulated annealing can only provide approximate answers and insights, which are nevertheless still useful.

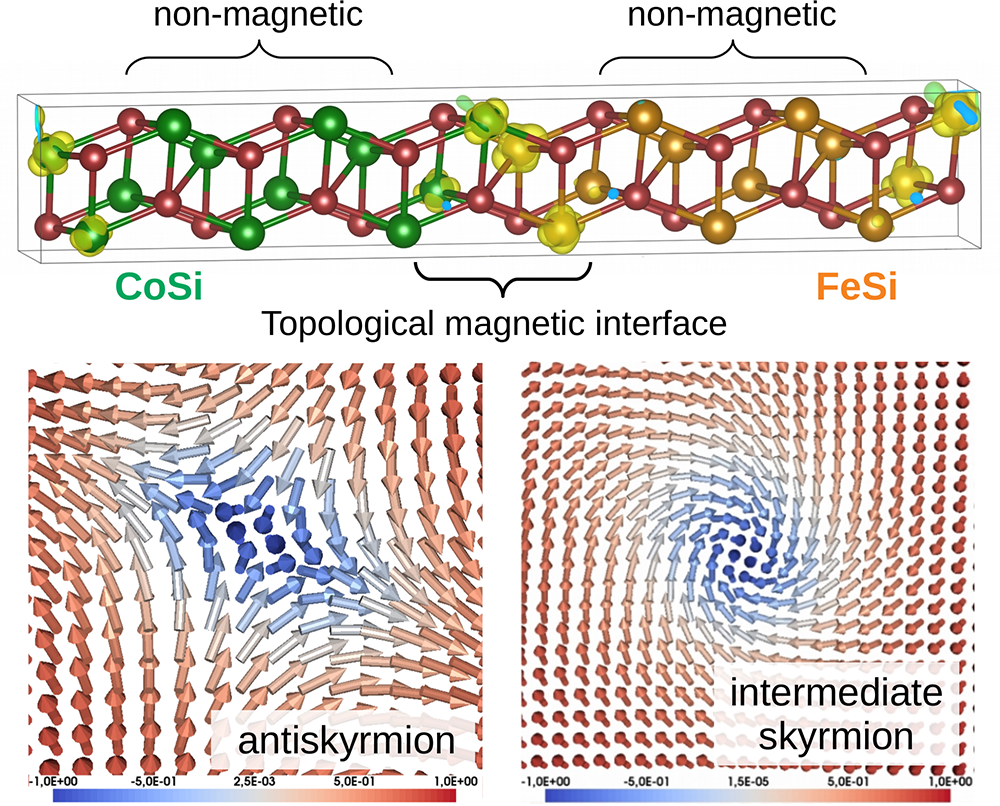
Another example is from a recent study [10] which makes predictions for multilayers formed from the B20 compounds FeSi and CoSi (see figure below) that have not yet been confirmed experimentally. Theory suggests that, although neither compound shows any long-range magnetic order in bulk, the presence of nanoscale interfaces in FeSi/CoSi structures leads to the emergence of magnetic order near the interfaces. Furthermore, even though bulk FeSi and CoSi are already chiral in the bulk, their chirality properties are modified considerably by the interface effects, leading to stabilisation of topological magnetic textures of different sorts: antiskyrmions, intermediate skyrmions and antiferromagnetic skyrmions (some of which are shown in the figure above). This variety can be traced back to the structure of chiral magnetic interactions calculated using the LKAG approach, which turns out to be very different from what is typically observed in B20 magnets, such as FeGe. Different possibilities for topological magnetism in these systems were explored in [10] via extensive atomistic spin dynamics for different B20 multilayers using the UppASD software and large simulation cells with 875,000 to 2,000,000 spins, depending on the interface configuration being studied. This motivates future experiments and studies of similar nanostructures with emergent interface phenomena.

It is noteworthy that from spin dynamics simulations one can not only get the picture of atomic spins in real space forming different magnetic patterns (ferromagnetic, antiferromagnetic or non-collinear ones, as shown in the figures on page 4 and to the left) but also obtain information on magnetic correlations and excitations in the system that can be compared with experiment. This comparison is important for validating the accuracy of the constructed effective spin model and theory approximations, in general.

3. Micromagnetics

Despite the power of the spin dynamics method, it has limitations in terms of the system size that can be simulated within a reasonable computational time. On modern supercomputer architectures, it is feasible to simulate spin systems with up to a few million spins, where simulated annealing may take up to a few weeks of computational time, depending on the complexity of magnetic interactions. To overcome these limitations and increase the length scale of simulations, one can switch to the micromagnetic description where the magnetisation in the material is assumed to vary slowly between neighbouring atomic spins and is effectively treated as a continuous variable. At the same time, the LLG equation is used to describe the magnetisation dynamics at finite temperature, just with different system parameters (like spin stiffness, DM spiralisation, and magnetisation density) that can be calculated from the atomistic interactions and properties. The size of the system that can be simulated micromagnetically is larger (above several micrometres) than the upper limit for the atomistic spin dynamics. However, the atomistic approach is more accurate and general, while the micromagnetic approach is limited to systems with slowly varying magnetisation.

These images show the crystal structure (a) and the two magnetic phases: spin spiral (b) and skyrmions (c) in lacunar spinel GaV₄S₈. The images are reproduced from [11].

One example is discussed in the theoretical study [11] of multiferroic skyrmionic spinel GaV₄S₈ (see figure above) which is known to host Néel skyrmions of around 20 nm size in bulk, a rather unique property of lacunar spinels [12]. The goal of that work was to understand the magnetic state of the V4 clusters which play the role here of effective spins interacting through the Heisenberg and Dzyaloshinskii-Moriya interactions that are usually also important for other topological magnets [13]. By calculating the micromagnetic parameters from first-principles atomistic data for two cluster configurations, which is widely discussed in the literature, it was found that the DM interaction is more pronounced in the so-called distributed-moment state where all V sites have a sizeable magnetic moment. The micromagnetic simulations for the two cluster states showed that this distributed-moment state much better supports the spin spiral and Néel skyrmions observed in experiments. The two visualisations on the right of the figure above indicate that simulated annealing in micromagnetic simulations does not lead to the lowest-energy state (ground state) but to a local energy minimum which can be fairly close to the ground state. For example, instead of an ordered skyrmion lattice, individual skyrmions are obtained at different positions, dependent on the initial random magnetic configuration. However, further analysis demonstrated that setting the local magnetic anisotropy to zero and annealing the magnetic state can actually stabilise a relatively ordered periodic skyrmion lattice, which preserves its structure even after the local anisotropy is restored in the simulation. This means that approaching the lowest energy state for a given magnetic system is highly non-trivial and depends on the value of magnetic interactions that can create energy barriers between different local energy minima. Despite this issue, analysing local energy minima obtained routinely in atomistic spin-dynamics and micromagnetic simulations can provide useful information on the magnetic properties that are realised in the studied material, as discussed in this article for the examples of Mn/W(110) bilayer [3], B20 multilayers [10] and GaV₄S₈ spinel [11].

Importantly, multiscale methods [14] can be applied where different parts of a given magnetic system are described either atomistically (for example, regions around point defects) or micromagnetically (the rest of the system) and the two descriptions are smoothly connected. This powerful combination of methods increases the accuracy and computational efficiency of modelling complex magnetic systems and makes it possible to discover qualitatively new phenomena (see [14]).

To summarise, the scale-bridging approach developed by a vast research community enables the modelling of magnetic materials on different length scales where model parameters are material-specific and effectively originate from accurate quantum-mechanical descriptions of the underlying crystal lattice. This approach takes full advantage of modern CPU- and GPU-based supercomputing architectures, the performance of which makes it possible to simulate realistic material models and push the boundaries of materials science.

Acknowledgements

Fruitful discussions with Dr. Olle Eriksson and Dr. Anna Delin are gratefully acknowledged.

References

1. O. Eriksson, A. Bergman, L. Bergqvist, J. Hellsvik, “Atomistic Spin Dynamics: Foundations and Applications, Atomistic Spin Dynamics: Foundations and Applications”, Oxford University Press, Oxford, UK, 2017.
2. A. Szilva, Y. Kvashnin, E. A. Stepanov, L. Nordström, O. Eriksson, A. I. Lichtenstein, M. I. Katsnelson, “Quantitative theory of magnetic interactions in solids”, Rev. Mod. Phys. 95, 035004 (2023).
3. V. Borisov, “From electronic structure to magnetism and skyrmions” (Invited Topical review), Electron. Struct. 6, 023002 (2024).
4. G. Kotliar, S. Y. Savrasov, K. Haule, V. S. Oudovenko, O. Parcollet, C. A. Marianetti, “Electronic structure calculations with dynamical mean-field theory”, Rev. Mod. Phys. 78, 865 (2006).
5. V. Borisov, Y. O. Kvashnin, N. Ntallis, D. Thonig, P. Thunström, M. Pereiro, A. Bergman, E. Sjöqvist, A. Delin, L. Nordström, O. Eriksson, “Heisenberg and anisotropic exchange interactions in magnetic materials with correlated electronic structure and significant spin-orbit coupling”, Phys. Rev. B 103, 174422 (2021).
6. A. I. Liechtenstein, M. I. Katsnelson, V. P. Antropov, V. A. Gubanov, “Local spin density functional approach to the theory of exchange interactions in ferromagnetic metals and alloys”, J. Magn. Magn. Mater. 67, 65 (1987).
7. J. M. Wills, B. R. Cooper, “Synthesis of band and model Hamiltonian theory for hybridizing cerium systems”, Phys. Rev. B 36, 3809 (1987).
8. J. M. Wills, O. Eriksson, P. Andersson, A. Delin, O. Grechnyev, M. Alouani, “Full-potential electronic structure method, in Energy and Force Calculations with Density Functional and Dynamical Mean Field Theory”, Springer Series in Solid-State Science Vol. 167 (Springer, Berlin, Heidelberg, 2010).
9. P. Ferriani, K. von Bergmann, E. Y. Vedmedenko, S. Heinze, M. Bode, M. Heide, G. Bihlmayer, S. Blügel, R. Wiesendanger, “Atomic-scale spin spiral with a unique rotational sense: Mn monolayer on W(001)”, Phys. Rev. Lett. 101, 027201 (2008).
10. V. Borisov, A. Delin, O. Eriksson, “Tunable topological magnetism in superlattices of nonmagnetic B20 systems”, Phys. Rev. B 110, L060407 (2024), Editors’ Suggestion Letter.
11. V. Borisov, N. Salehi, M. Pereiro, A. Delin, O. Eriksson, “Dzyaloshinskii-Moriya interactions, Néel skyrmions and V4 magnetic clusters in multiferroic lacunar spinel GaV4S8”, npj Computational Materials 10, 53 (2024).
12. I. Kézsmárki, S. Bordács, P. Milde, E. Neuber, L. M. Eng, J. S. White, H. M. Rønnow, C. D. Dewhurst, M. Mochizuki, K. Yanai, H. Nakamura, D. Ehlers, V. Tsurkan, A. Loidl, “Néel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor GaV4S8”, Nat. Mater. 14, 1116- 1122 (2015).
13. N. Kanazawa, S.
14. “Noncentrosymmetric magnetic skyrmions”, Adv. Mater. 29, 1603227 (2017).
15. É. Méndez, M. Poluektov, G. Kreiss, O. Eriksson, M. Pereiro, “Multiscale approach for magnetization dynamics: unraveling exotic magnetic states of matter”, Phys. Rev. Research 2, 013092 (2020).