Describing Connectivity in Neuronal Network Models
Mikael Djurfeldt, PDC
PDC has recently participated in a project that aimed to improve descriptions of connectivity in neuronal network models. The results have been published in a paper in the journal Public Library of Science (PLOS) Computational Biology [3]. This work was motivated by the ongoing reproducibility crisis in science [4], which also applies to the specific field of computational neuroscience (see, for example, [5]). One of the reasons why results in this field often cannot be reproduced is that the descriptions of the sometimes rather complex simulated models are insufficient and/or ambiguous to such an extent that they cannot be re-implemented.
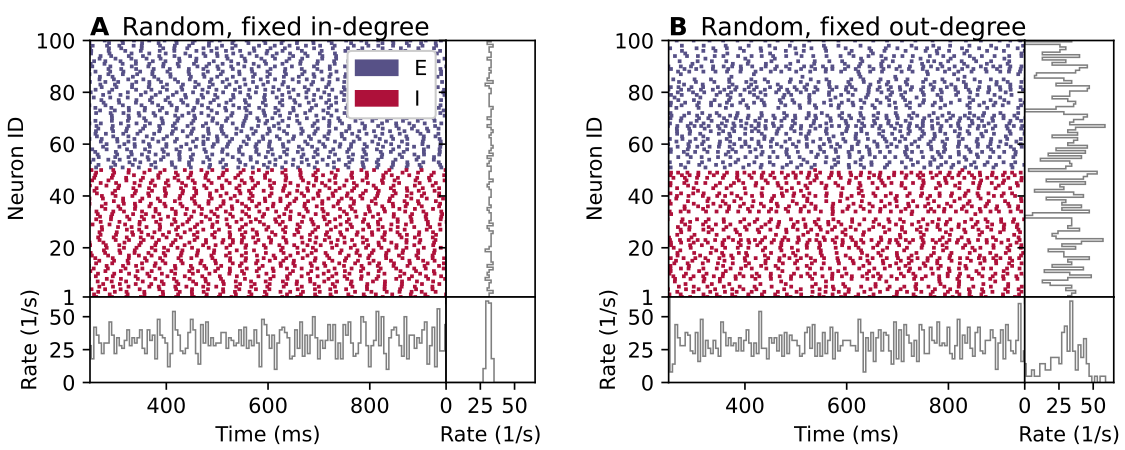
This is illustrated by the figure below, which shows raster plots of neuronal signalling events (“spikes”) of two neuronal networks with “random” connectivity. In part A of the figure, each neuron receives a fixed number of incoming connections from randomly selected pre-synaptic neurons, while in part B each neuron provides connections to a fixed number of randomly selected post-synaptic neurons. Although both networks have “random” connectivity and everything else is equal, the two networks display both different network structure and different dynamics. Clearly, the statement that a neuronal population is connected randomly to another is ambiguous.
The project began with a review of published network models where the implementation of the model could be found in one of the online repositories ModelDB [6] and Open Source Brain [7]. Ambiguous network model descriptions were found in 15 out of the 42 publications that were examined. We also reviewed a set of model description languages, which included those specific to a simulator and those available on multiple platforms. Based on the review, we identified a set of recurring concepts used in network connectivity descriptions and suggested guidelines for how a network could be described unambiguously using mathematics or text, and also provided a graphical notation which can be used to unambiguously describe networks in illustrations.
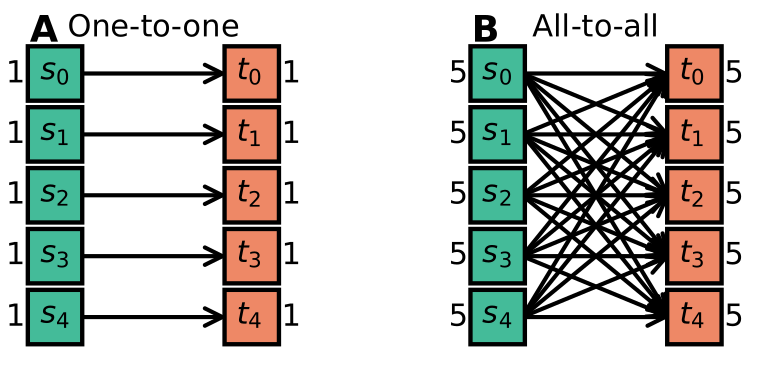
Some examples of concepts that were identified are one-to-one connectivity, where each source neuron is connected to one target neuron (which only receives a connection from that source) and all-to-all connectivity, where each source neuron is connected to every target neuron (see the figure below).
For the mathematical description of connectivity, the Connection-Set Algebra (CSA) [1] was used. It is a mathematical formalism for describing network connectivity using elementary sets of connections and set operators. It has parallelised implementations which help a neuronal simulator instantiate a CSA network description efficiently [2]. This makes CSA suitable for highly scalable brain simulations.
In CSA, a connection is represented by a pair of indices (i, j) which refer to the entities being connected, usually neurons: i is the source neuron and j the target neuron. A connection pattern can then be described as a set of pairs of indices. In CSA it turns out to be fruitful to work with infinite sets of indices. For example, the elementary connection set δ = {(0, 0), (1, 1), …} can be used to describe one-to-one connectivity in general, regardless of source and target population size. We can then work with CSA operators on infinite connection sets to extract the actual, finite, connection pattern at the end. Given the (finite) sets of indices ℕS and ℕT of the source and target neuron populations S and T, we can extract the finite one-to-one connection pattern between them through the expression δ ∩ (ℕS × ℕT) where ∩ is the set intersection operator and × is the Cartesian product.
Another example of an elementary connection set is the set of all connections Ω = {(0, 0), (0, 1), …, (1, 0), (1, 1), …} (where indices in both source and target positions run over all natural numbers). Note that if S = T (connections go from the population onto itself), it is immediately possible to express all-to-all connectivity without self-connections as Ω − δ where − is the set difference operator. With its limited set of elementary sets and operators, CSA is surprisingly expressive. There are also implementation strategies which handle the infinite sets well.
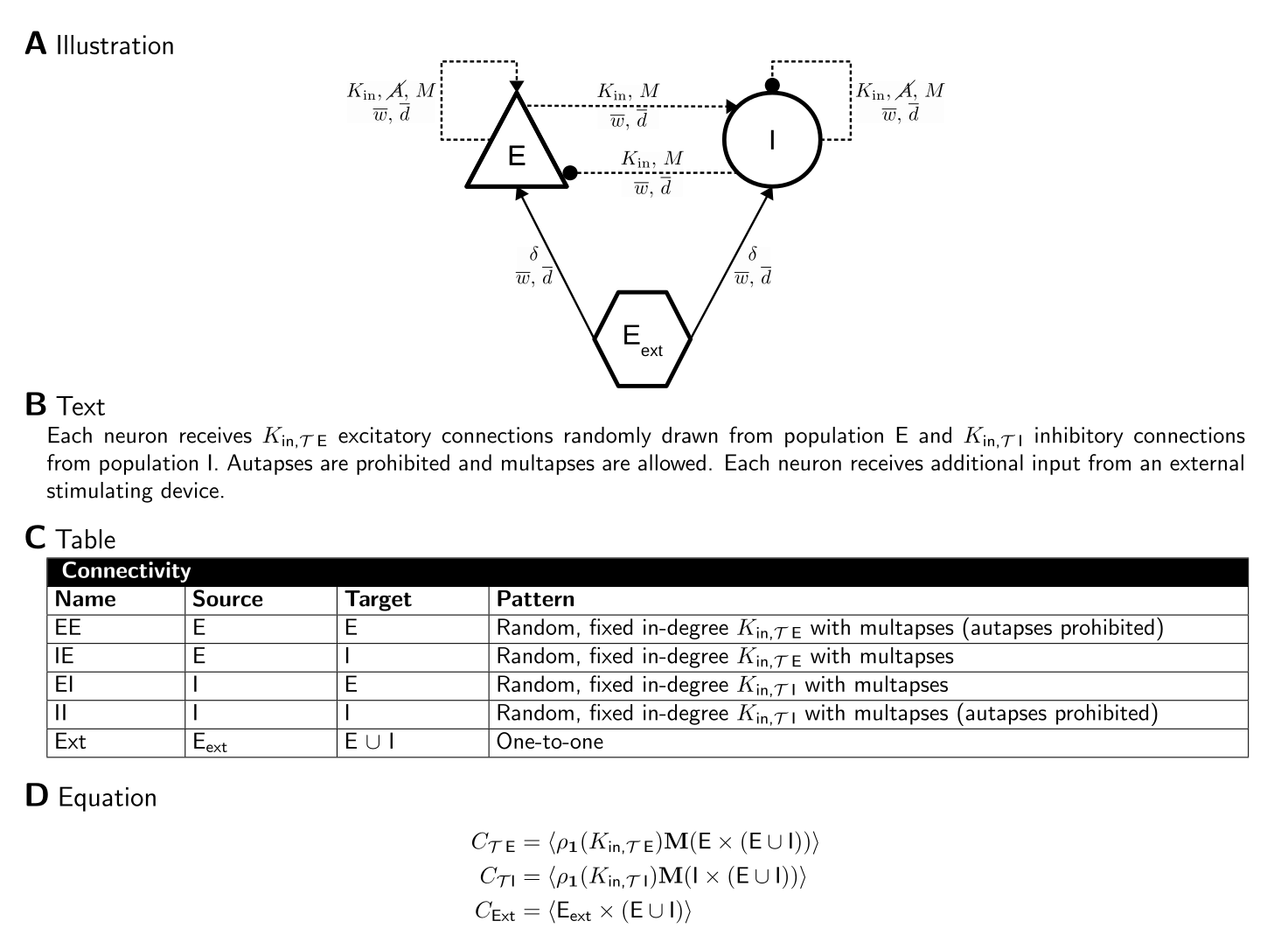
The figure below shows an example network where the network connectivity is described in four ways, as a graph using our proposed graphical language, as text, as a table and as CSA equations. For details, see [3].
We regard this work as a starting point for discussion. The language and notation that we propose are mostly appropriate for a common class of deterministically and probabilistically connected networks that we find in the literature, and we also, to some extent, address networks embedded in metric space. The notations that are proposed will need to be extended to cover other domains and levels. Nevertheless, we hope that our methods will inspire further work and discussion. An advantage of the CSA notation is that it is readily transferred to software that can instantiate the network with good scaling on a supercomputer.
References
- M. Djurfeldt, The Connection-set Algebra—A Novel Formalism for the Representation of Connectivity Structure in Neuronal Network Models. Neuroinform. 2012, 10, 287–304. doi.org/10.1007/s12021-012-9146-1
- M. Djurfeldt, A.P. Davison, and J.M. Eppler, Efficient generation of connectivity in neuronal networks from simulator-independent descriptions. Frontiers in Neuroinformatics. 2014, 8:43. doi.org/10.3389/fninf.2014.00043
- J. Senk, B. Kriener, M. Djurfeldt, N. Voges, H.‑J. Jiang, L. Schüttler, et al., Connectivity concepts in neuronal network modeling. PLOS Computational Biology. 2022, 18(9), e1010086. doi.org/10.1371/journal.pcbi.1010086
- J.P. Ioannidis, Why most published research findings are false. PLOS Medicine. 2005 August, 2(8), e124. doi.org/10.1371/journal.pmed.0020124 . Epub 2005 August 30. Erratum in: PLOS Medicine 2022 August 25, 19(8), e1004085. PMID: 16060722; PMCID: PMC1182327.
- S.M. Crook, J.A. Bednar, S. Berger, R. Cannon, A.P. Davison, M. Djurfeldt et al., Creating, documenting and sharing network models. Network: Computation in Neural Systems. 2012, 23(4), 131–149. doi.org/10.3109/0954898X.2012.722743 PMID: 22994683
- B.E. Peterson, M.D. Healy, P.M. Nadkarni, P.L. Miller, G.M. Shepherd, ModelDB: An Environment for Running and Storing Computational Models and Their Results Applied to Neuroscience. Journal of the American Medical Informatics Association. 1996, 3(6), 389–398. doi.org/10.1136/jamia.1996.97084512 PMID: 8930855
- P. Gleeson, M. Cantarelli, B. Marin, A. Quintana, M. Earnshaw, S. Sadeh et al., Open Source Brain: A Collaborative Resource for Visualizing, Analyzing, Simulating, and Developing Standardized Models of Neurons and Circuits. Neuron. 2019, 103(3), 395–411.e5. doi.org/10.1016/j.neuron.2019.05.019 PMID: 31201122
- E. Nordlie, M.O. Gewaltig, H.E. Plesser, Towards Reproducible Descriptions of Neuronal Network Models. PLOS Computational Biology. 2009, 5(8), e1000456. doi.org/10.1371/journal.pcbi.1000456 PMID: 19662159