Dynamics of Magnetic Materials
Anders Bergman, Anna Delin, Manuel Pereiro, Erik Sjöqvist, Danny Thonig & Olle Eriksson, Department of Physics and Astronomy, Uppsala University
Introduction
Magnetism and magnetic excitations of solids have traditionally been analyzed by two seemingly different approaches: electronic structure theory based on density functional theory [1,2] and the Heisenberg Hamiltonian [3]. The former has been used to calculate (in ab initio fashion) the magnetic moments, the easy axis magnetization and the magnetic ordering [4] of solids, while the latter is typically used to analyze magnon (or spin wave) dispersions and to estimate ordering temperatures [5]. The Heisenberg Hamiltonian, and modifications of it, have also been adopted to provide microscopic understanding of exotic magnetic phenomena, such as spin-glass formation [6], as well as the Kosterlitz-Thouless transition [7]. Analyzing magnetic phenomena by means of the Heisenberg Hamiltonian has proven to be extremely successful, with the gnawing shortcoming of being a parametrized theory: the interactions used in this Hamiltonian have hitherto been fitted to experimental data or guessed.
These two seemingly disparate approaches have recently been merged into what may best be described as a multiscale approach for evaluating basically all magnetic phenomena from one common platform. This article describes the essentials of this approach, and provides numerical examples of calculating magnetic ground state properties (as well as results for the excited state) for a range of materials. The theoretical toolkits that have emerged from these considerations are now available in software [8,9] that is installed at all Swedish National Infrastructure for Computing (SNIC) supercomputer centres. The theory is therefore ready to tackle any challenge associated with new and exotic magnetic phenomena, such as those that will emerge from large scale facilities like the European Spallation Source (which is a multi-disciplinary research facility currently being constructed to provide unique information about the structure and properties of biology, chemistry, physics, and engineering materials by using what will be the world's most powerful pulsed neutron source).
Atomistic Spin Dynamics
The accuracy of Density Functional Theory (DFT) calculations and the efficiency of analyzing magnetism using the Heisenberg Hamiltonians can be combined with the atomistic spin dynamics method (ASD) [10]. As the name indicates, the quantum-mechanical spin density that originates from the distribution of the electrons in the material is treated on an atomic level. This is done by assuming a model where each atom i is associated with a local magnetic moment, described as a vector, mi. The interplay between the local moments is then described with the Heisenberg model. This model is based on pair-interactions, Jij, betw1een moments mi and mj on sites i and j, so that the energy can be written as
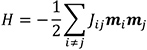
In this context, the pair-interactions are called exchange interactions since they stem from the energy associated with exchanging spins in a system, according to the Pauli exclusion principle. The Heisenberg model can be considered in a fully quantum mechanical fashion, where mi represents a spin operator on site i, multiplied by the g-factor. Here we will adopt a classical (or semi-classical) approach, where mi represents the magnetic moment at site i, and the moment can point in any direction. Assuming that the semi-classical Heisenberg model can provide an adequate approximation of a system, the critical part for obtaining a realistic and material-specific description is to determine the exchange interactions Jij accurately. This is where the coupling to DFT calculations enters since there now exist several methodologies to calculate the needed set of exchange interactions for almost any material.
With a realistic Heisenberg model, the energy for any given magnetic configuration (that is, any ensemble of directions of the moments in the system) can be accurately calculated for large systems containing billions of atomic moments. This can be used in combination with nite- temperature Monte Carlo simulations to determine the magnetic ground state of the system, as well as phase transition temperatures (in other words, temperatures at which the system changes from an ordered to a disordered state).
In order to properly describe excited states of magnetic materials (that is, what happens to a magnet when an external field, a laser pulse, or an electric current is applied), one needs to describe the magnetization dynamics (which means the time dependence of the magnetic moments). As has been shown – both from equivalents to phenomenological theories and rigorous derivations from first principles – the local magnetic moments follow an equation of motion that depends on the effective magnetic field that acts on each moment. The equation of motion for the moments can be written as
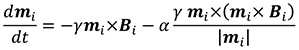
which is an atomistic version of the Landau-Lifshitz-Gilbert (LLG) equation. Normally it is formulated on a macro-spin level, and is then used to describe the magnetization on a more coarse-grained level. In the atomistic LLG equation, the gyromagnetic ratio γ and the Gilbert damping α also come into play, where the latter determines the rate of dissipation of energy and angular momentum. The remaining quantity to be determined is the effective magnetic field Bi which can be obtained from the Hamiltonian as Bi = -∂H/(∂mi). Temperature effects can be included in the magnetization dynamics by means of Langevin dynamics which are obtained by adding temperature-dependent stochastic contributions to the effective field.
These atomistic spin dynamics have been implemented, together with a collection of Monte Carlo routines and related functionalities, in the code UppASD, available at [9], which runs readily on high-performance computing (HPC) resources available at PDC and other SNIC centres. The algorithms have been parallelized using both OpenMP and MPI, and can also run efficiently on GPU resources. However, due to the efficient formulation and implementation of the method, it is possible to run the majority of simulations on a single node/workstation.
The ASD framework can be used to extract a multitude of relevant physical properties for magnetic systems. As mentioned earlier, the critical temperature where a phase transition will occur is one of these central properties. Studies of real-time dynamics can also be done with ASD. Notable examples of this include simulations of complex ultrafast demagnetization processes that occur when materials are exposed to high-fluency laser pulses and studies of the dynamics of topological magnetic solitons in the presence of electric currents and magnetic fields. In this article, we highlight a few examples of previous and ongoing studies of relevant magnetization dynamics where UppASD has been employed: magnon and skyrmion dynamics.
Magnetic Excitations
In recent years, the magnetism of ultrathin films on certain substrates has become experimentally accessible, in particular, by means of spin-polarized electron energy loss spectroscopy (SPEELS) or scanning-tunnelling microscopes (STM). This has been an important development, since it provides the means to extract magnetic excitation energies from nano- sized samples, which more traditional methods (like neutron scattering) cannot do. Examples of such ultrathin films are a single atomic layer (monolayer or ML) of Co on Cu(001) [11], Fe on Cu(001) [12] or multiple layers (1-5 ML) of Fe on W(110)[13]. Experimental accessibility to these systems has been opening up new views on whether the semi-classical atomistic model discussed earlier is accurate enough to describe the experimental trends or to even predict magnetism in different materials.
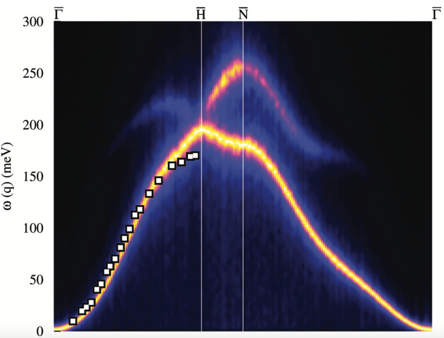

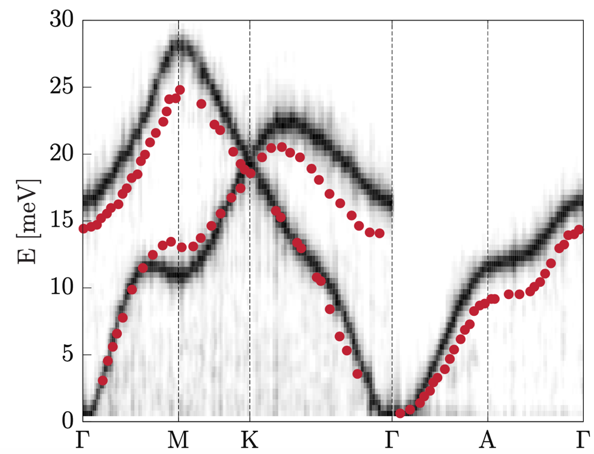
Magnetism in ultrathin magnetic films can show exotic ground states arising from finite temperature and relativistic spin-orbit coupling effects. These effects also cause unexpected dynamics of the atomistic magnetic moments and an anisotropic magnon propagation. Magnons are collective, quasi-particle wave excitations of the atomistic magnetic moments [10]. They carry a certain energy ω related to the precession frequency of the individual spins in a spin wave, as well as momentum q related to the wave length and the propagation direction of the magnon. The relation between the energy and momentum of a magnon, known as magnon dispersion ω(q), can be measured in the SPEELS experiments mentioned previously and is a measure of the exchange interactions between the atomic magnetic moments. The magnon dispersion is, coincidentally, one measurable for which ASD is perhaps the best-suited theoretical tool. As a showcase, we have studied magnons in 2 ML Fe on W(110) [14] (see figures above) and in the lanthanide Gd [15] (see figure below) and achieved not only excellent qualitative, but also quantitative, agreement with experimental results.
For both of our examples, the interactions between the atomistic spins were calculated from first-principle DFT methods, where the only parameter to the simulation is the lattice constant of the crystal structure. When these interactions were included in our spin dynamics simulations, we observed a softening of the magnons for 2 ML Fe/W(110) with respect to the Fe-bulk spin wave dispersion. This is the result of weaker interactions between the atomic magnetic moments due to a lower level of coordination at the surface. Furthermore, our calculations revealed that spatial-anisotropic interactions (the so-called Dzyaloshinskii-Moriya interactions) are present in 2 ML Fe/W(110) and that they cause an asymmetry, in other words, ω(q) differs from ω(-q) around the Γ-point in the magnon dispersion, which represents the case where all spins have coherent precession. This asymmetry depends strongly on the magnon momentum (shown in the second of the pair of figures above), which was first measured in SPEELS experiments [17] (blue dots) and later confirmed by our model (red dots).
As a second example, we focused on the magnetism of lanthanides, with gadolinium (Gd) as a representative of this class. Lanthanides are particular due to the localization and correlation of the electrons that are responsible for the magnetism (the 4f shell). As a consequence, the interaction between the magnetic moments is weak since it is related to the small wave function overlap of the 4f shell of two separate lanthanide atoms. This makes it demanding to calculate with first principle methods, due to the high computational precision needed to calculate the interaction and hence the respective magnon dispersion (see the figure above). The dispersion is seen to follow a parabolic dependence. This is clear evidence of the colinear ferromagnetic ordering, which is intrinsic to Gd at low temperatures. As in our previous example, we obtained excellent agreement between experiment (red dots) and theory (gray background), which highlights the high quality of the interactions obtained between the magnetic moments in Gd, as well as the accuracy in extracting the magnon dispersions from ASD simulations.
Topological Magnets
The presence of defects or other symmetry-breaking inclusions can strongly influence dynamical properties at both microscopic and macroscopic length scales. The ASD framework is ideally suited for resolving the magnetization at an atomic level but in order to access more mesoscopic length scales (which here means little more than a micrometer scale), one needs to include another level of multiscale simulations. We have recently implemented a multiscale method [19] capable of bridging atomic and micrometer length scales. This technique is capable of solving the Landau-Lifshitz-Gilbert equations efficiently in two regions of a magnetic material – the mesoscopic and the atomistic regions, which are coupled in a seamless way. The method has initially been applied to studies of topological magnets where magnetic whirls, called skyrmions, can occur. Skyrmions have many intriguing properties, including ideally topological protection and a particle-like behaviour, and have been touted as a viable basis for future data processing technologies. Our multiscale study on the transport behaviour of skyrmions in the presence of defects is best presented in the video at https://play.kth.se/media/PDC+Newsletter+2020+No.+2A+Dynamics+of+Magnetic+Materials+-+supplementary+video/0_wxolmrm2 .
Quantum Information
A central concept in quantum information science and technology is the possibility to create and manipulate quantum entanglement. This purely quantum-mechanical feature implies stronger-than-classical correlations that can persist over long distances and even in noisy environments, such as in the case of excitation energy transfer in biological systems. It is used as a resource in quantum communication and is a key ingredient for the quantum parallelism that is used in quantum computers.
Driven by potential applications for information technology, there is a growing recent interest in finding methods to prepare, control, and verify entanglement amongst collective modes in the solid state. In particular, magnons can show entanglement and can also entangle with other degrees of freedom, such as phonons and photons.
A long-term goal of our research is to explore how magnonic degrees of freedom can be used in hybrid settings, involving other quantum-mechanical degrees of freedom, for building quantum networks for quantum information processors and quantum communication devices. In particular, we have in mind a new form of hardware for quantum computation in materials – a quantum version of “magnonics” – where entangling logical gates between localized qubits can be mediated by means of entangled magnon-pairs.
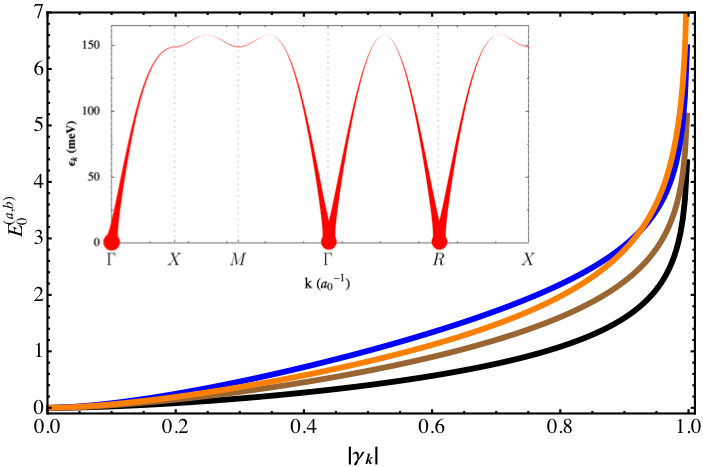
Antiferromagnets are candidate systems for magnon entanglement, as their magnetic spin lattice naturally divides into a pair of sublattices. In a paper by Azimi Mousolou et al. [20], it has recently been demonstrated that these sublattices are indeed entangled, even in the vacuum state where no magnons are present. This mode entanglement is a quantifiable resource (see the figure below) that can be very large, in particular for long-wavelength magnon modes. To show this, we have considered a generic lattice of spins with Heisenberg and Dzyaloshinskii-Moriya interaction, as well as anisotropy terms, for which an intricate layer of entanglement between the two sublattices can be seen. This intrinsic entanglement of the antiferromagnet can potentially be tested by letting the collective spin modes interact with an external source of, for example, photons or photon polarization, which can be measured by techniques known in quantum optics. In this way, the magnon mode entanglement can not only be tested experimentally, but can also act as a resource for photon entanglement. This particular study was performed using analytical methods based on the Heisenberg model but ASD studies on these materials are forthcoming.
Outlook
Looking forward, we believe that spin dynamical phenomena will come to play an important role in the development of several key future hardware technologies for computing. The time-integrated amount of stored information is doubling roughly every eighteen months and, since the majority of the world's information is stored in magnetic media, the possibility to write information to (and retrieve information from) a magnetic material at ever greater speed, and with lower energy consumption, has obvious bene ts for our society. Hence the seemingly simple switching of a magnetic unit – a magnetic bit – is a crucial process which de nes how e ciently information can be stored and retrieved from a magnetic memory. From an application point of view, it is apparent that it is advantageous to be able to switch the magnetization of a bit as fast as possible while minimizing energy losses. All-optical control of magnetism has for this reason become an intense research field, with reports on remarkably fast switching times. Surprisingly, the mechanism behind the ultrafast switching is still unknown. Our recent work that connects the spin motion and lattice vibrations [21] aims to answer this question.
Topological magnets such as skyrmions have also been mentioned as promising for future magnetic memories and in addition they have other properties which make them suitable for related processes. Neuromorphic computing, where features of the human brain are used as inspiration for efficient data processing, is currently becoming an increasingly active field of research. Magnetization dynamics play a central role in spintronic-based neuromorphic computing [22]. Here, magnetic topological textures such as skyrmions or domain walls take the role as neurons and magnetic tunnel junctions can function as both synapses and neurons.
As indicated in the Engtanglement section earlier, quantum entanglement in magnetic materials can be used to link several small quantum processors for large-scale quantum computing and also for interfacing a quantum computer, for example, arrays of spins or ions, with optics for long-distance quantum communication [23].
References
- P. Hohenberg, W. Kohn, Phys. Rev. 136, B864- 871 (1964)
- W. Kohn, L. Sham, Phys. Rev. 140 A1133-1138 (1965)
- See e.g. N. Ashcroft and D. Mermin, Solid State Physics, Saunders College Publishing (1976)
- J. Kubler, Theory of itinerant electron magnetism, Oxford Science Publications (2000)
- D. Landau, K. Binder, A guide to Monte Carlo simulations in Statistical Physics, Cambridge University Press (2005)
- G. Parisi, P. Urbani, F. Zamponi Theory of Simple Glasses. Cambridge University Press (2020)
- J.M. Kosterlitz, D.J. Thouless, Ordering, metastability and phase transitions in two- dimensional systems. Journal of Physics C: Solid State Physics. 6 (7): 1181–1203 (1972)
- www.physics.uu.se/research/materials-theory/ongoing-research/code-development/rspt-main
- www.physics.uu.se/uppasd , github.com/UppASD/UppASD
- O. Eriksson, A. Bergman, L. Bergqvist and J. Hellsvik, Atomistic Spin-Dynamics, fundamentals and applications (Oxford university press, 2017)
- R. Vollmer et al., Phys. Rev. Lett. 91, 147201 (2003)
- S.Achillietal., J.Phys.Cond.Matt. 19305021 (2007)
- J. Prokop et al., Phys. Rev. Lett. 102, 177206 (2009)
- L.Bergqvist, A.Taroni, A.Bergman, C.Etz, and O. Eriksson, Phys. Rev. B 87 144401 (2013)
- I. L. M. Locht, Y. O. Kvashnin, D. C. M. Rodrigues, M. Pereiro, A. Bergman, L. Bergqvist, A. I. Lichtenstein, M. I. Katsnelson, A. Delin, A. B. Klautau, B. Johansson, I. Di Marco, and O. Eriksson, Phys. Rev. B 94 085137 (2016)
- W. X. Tang et al., Phys. Rev. Lett. 99, 087202 (2007)
- Kh. Zakeri et al., Phys. Rev. Lett. 104, 137203 (2010)
- J. Jensen and A. R. Mackintosh, Rare Earth Magnetism (Clarendon Press, Oxford, U.K., (1991)
- E. Mendez, M. Poluektov, G. Kreiss, O. Eriksson, and M. Pereiro. Phys. Rev. Research 2, 013092 (2020)
- V. Azimi Mousolou, A. Bagrov, A. Bergman, A. Delin, O. Eriksson, Y. Liu, M. Pereiro, D. Thonig, and E. Sjöqvist, https://arxiv.org/ abs/2006.03479 (2020)
- J. Hellsvik, D. Thonig, K. Modin, D. Iuşan, A. Bergman, O. Eriksson, L. Bergqvist, and A. Delin, Phys. Rev. B 99, 104302 (2019)
- S. Bose, PRL 91, 207901 (2003)
- J. Grollier et al., arXiv:2007.06092 (2020)
Note
Anna also works at the Department of Applied Physics, School of Engineering Sciences, KTH Royal Institute of Technology and the Swedish e-Science Research Centre (SeRC), KTH Royal Institute of Technology.
Danny and Olle also work at the School of Science and Technology, Örebro University.